This demo shows the action of the quantum fourier transform (which is itself a version of the discrete fourier transform).
- TOP: quantum state in register before QFT
- BOTTOM: quantum state in register after QFT
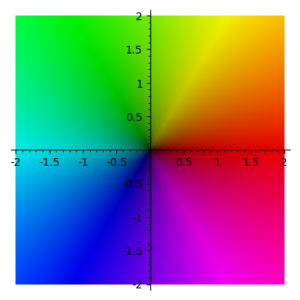
The complex coefficients of each classical state are represented as a coloured bar. The colour represents the phase, using the usual domain colouring standard as in the picture below (red = positive real direction, greeny-yellow = positive imaginary direction). The height represents the complex absolute value.
You can alter the input function with your keyboard:
- N/n to increase/decrease the value of N
- A/a to increase/decrease the value of a
- B/b to increase/decrease the value of b
- C/c to increase/decrease the value of c
- Q/q to increase/decrease the number of qubits
The input function is $$f(x) = N\left \{ \frac{c + bx}{N} \right \} e^{2\pi i a x / N}$$