Numberscope is a research and citizen-scientist tool to combine your favourite integer sequence with a suite of visualizers, software tools that illustrate integer sequences and their properties.
Contributors: Abdullatif Khalid Abduljaleel, Tobias Aldape, Khaled Allen, Isabel Anaya, Sebastian Bozlee, Brendan Heaney, Steven Hristopoulos, Ang Li, Theodore Lincke, Josiah Martinez, Willem Mirkovich, Liam Mulhall, Katherine Stange, Daniel H. Taylor and Glen Whitney.
The website is currently in development and will also include a way to contribute/adapt visualizers, as well as tools for calling sequences via OEIS number, formula, etc. A server backend caches sequences and provides access to pari to factor terms. You can view our progress at github. You can follow Numberscope on twitter for updates (currently very few, but when they happen you will know!).
This project is being put together under the leadership of Katherine E. Stange with the help of a large team of contributors, including undergraduates at via the Experimental Mathematics Lab at CU Boulder. This project wouldn’t be possible without the incredible skills and ideas of many people. We also thank ICERM for the support to work on this project during the Fall 2019 special semester on Illustrating Mathematics, and NSF for their support. We also owe a debt of gratitude to all the makers on the internet who have created stunning and interesting visualizations, many of which inspired this project.
PROJECT UPDATES:
June 6th, 2022: We have set a milestone to have the project set up for students to develop visualizers as part of the Math Lab in Fall 2022. Some recent developments: the project is licensed under the MIT License, and you can download and tinker with the code from github. The backend caches and factors (using postgres and pari) sequences requested from OEIS, and the frontend works with javascript bigint, and understands math formulas & OEIS numbers. Several visualizers are now included, including the chaos visualizer below. Major and important structural work has been done, including updating the framework, setting up proper workflow, linting, a test suite, etc. etc.
Play with our Example Visualizers!
The website is not yet available for public use. However, you can click below on some of the visualizers (often running on built-in sequences in these instances), to see proof-of-concept ideas for some of the visualization tools. These are works in progress!
Turtle on a Sequence
Turtle Walks use a sequence of integers, suitably parsed, as instructions for turning and walking on the plane. These are related to L-systems, and have some precursors on the web for Thue-Morse and p-adic valuations. A prototype was programmed by Abdul Abduljaleel, and this version by Katherine Stange.
Self-Similarity Telescope
The self-similarity telescope plots a sequence against various linear subsequences, highlighting moments of similarity. Similarity can mean nearby in size, or it can mean sharing factors, or similar valuation at a prime. The precursor to this tool is a Dot Plot in Bioinformatics (e.g. DNA), and a coprimality plot of the integers. This version was programmed by Katherine Stange; a prototype was programmed by Sebastian Bozlee.
Prime Filter
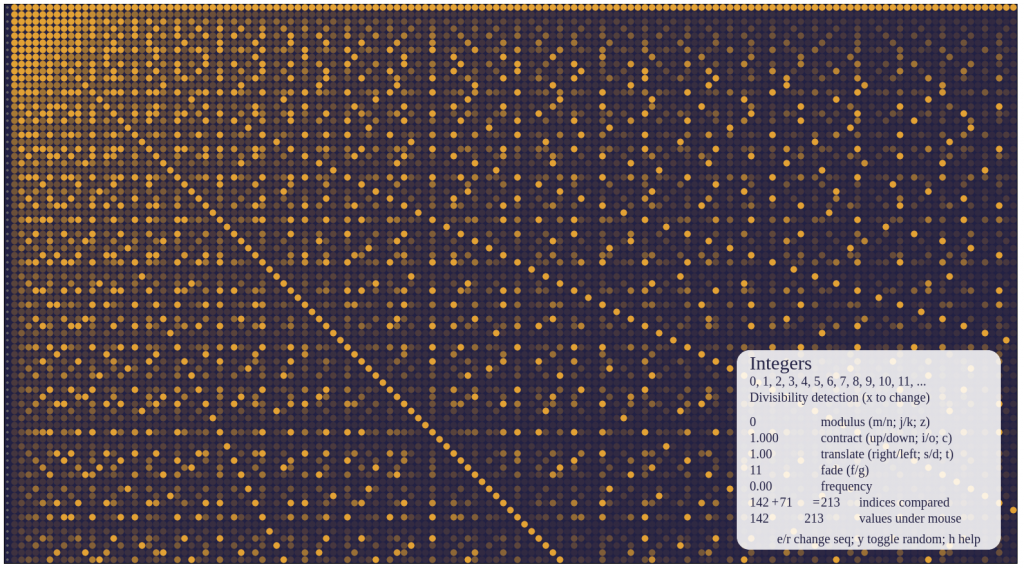
This tool shows a histogram whose domain is pairs (p,t) of primes p and translations t of the sequence in question. The function the histogram shows is a statistical measure of the occurrence of that prime in the sequence, e.g. total p-adic valuation of the sequence, or frequency of divisibility by p, etc. This was programmed by Katherine Stange. A prototype was programmed by Tobias Aldape.
Chaos Game (very rough)
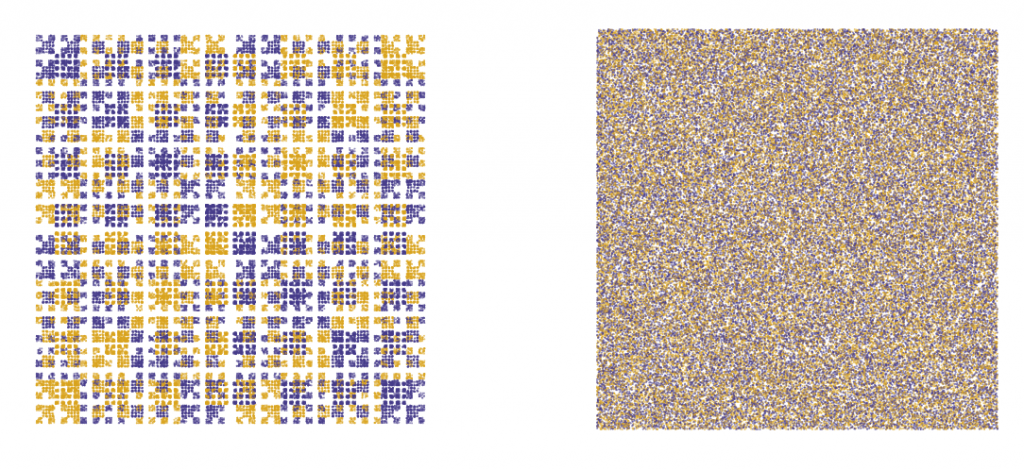
The Chaos Game uses the sequence modulo n to walk around inside a polygon, stepping a fixed ratio of the distance from the current location to the n-th corner of the polygon. The result of a random such walk is a fractal in most cases. In the case of the square, the result is a histogram of the frequency of certain substrings in a sequence, which was famously applied to primes, but originates with DNA analysis. A particularly beautiful implementation of the Chaos Game was created by Andrew Wang-Hoyer. Another interesting exploration is at betweenartandscience.com. This is programmed by Katherine Stange.
Some somewhat more prototype-y stuff
Shift Similarity
The position x,y shows whether the term indexed by x+y agrees with the term indexed by x. Code by Sebastian Bozlee. This was the precursor to the Self-Similarity Telescope above.
- Primes
- Racaman Sequence
- Fibonacci Numbers
- Elliptic Divisibility Sequence
- Thue Morse Sequence
- Elliptic Divisibility Sequence — this time comparing x with y (instead of x+y with y)
p-adic Lightning
The sequence is shown term by term as time progresses, as a p-adic expansion: the residue mod p is the first big “clock”, then the residue mod p^2 is the second level of “clocks” etc. Use Left/Right to change p (not necessarily prime), and Up/Down to change the scaling factor for the tree. Code by Sebastian Bozlee.
Factorization Solar Systems
The factorization of the number is shown using a variation on this method, for terms of the sequence in order. Code by Katherine Stange.
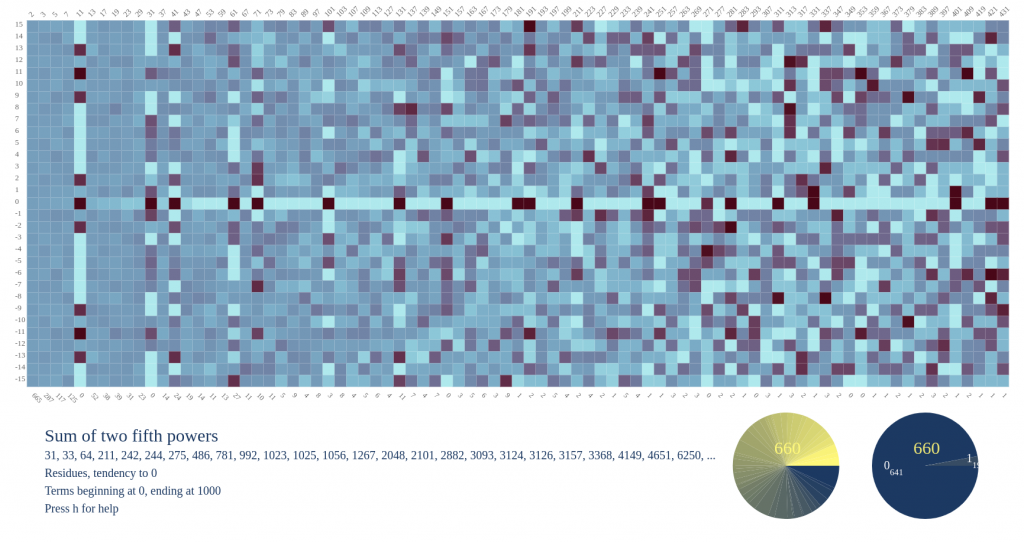
Residue Histograms
Each column corresponds to a modulus. That column is a histogram of the residues of the sequence, where white represents 0 and black represents that this residue did in fact get hit. The program draws as it walks up the sequence so you can see the histogram develop. Code by Tobias Aldape. This is a precursor to the Prime Filters tool above.
- Primes
- Curvatures in the Apollonian Circle Packing known as the “people packing” (which has a local obstruction modulo 24)
Turtle Walks or L-Systems
The terms of an integer sequence are interpreted as directions for a turtle walk, e.g. “one step”, “turn left 60 degrees” etc. Some screenshots are available to view, from Fibonacci sequences: Code by Abdul Abduljaleel. This is the precursor to the Turtle on a Sequence tool above.
Game of Life on a Hilbert Curve
The idea here is to seed Conway’s game of life using an integer sequence input on the plane along a Hilbert curve. Code by Daniel H. Taylor. Here are some screenshots.
Ulam Spirals
This marks an increasing sequence as a subset of the natural numbers, mapped onto a spiral. This is based on the famous Ulam spiral. Code by Tobias Aldape.
Some Inspiration
Here are some visualizers around the web that are particularly beautiful and interesting. In some cases, these inspired our own creations of visualizers.