This demo shows the steps of Shor’s Algorithm.
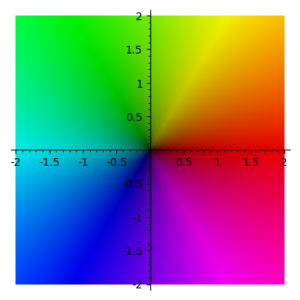
The complex coefficients of each classical state are represented as a coloured bar. The colour represents the phase, using the usual domain colouring standard as in the picture below (red = positive real direction, greeny-yellow = positive imaginary direction). The height represents the complex absolute value.
The screen shows two quantum superpositions:
- TOP: the first (and second) quantum register are shown in two lines of text
- BOTTOM: the QFT of the first superposition (see QFT demo)
Pressing C/c advances/retreats the steps of the algorithm. Recall that the goal of the algorithm is to find the period of the function $x \mapsto a^x \pmod N$, which can (classically) be turned into a factorization of $N$.
- Step 1: The qubits are in their intial states. The upper suposition is an evenly distributed superposition of the states $| x, 0 \rangle$.
- Step 2: The second register is computed. The states $| x, 0 \rangle$ become $| x, f(x) \rangle$, where $f(x) = a^x \pmod N$.
- Step 3: The second register is measured. This results in one value. All states not having this value in the second register are zeroed out.
Once at Step 3, you can look at the QFT below to see the resulting quantum state. This is the state you wish to measure to obtain the periodicity of $a^x \pmod N$.
Keyboard controls:
- C/c to advance/retreat the steps of the simulation
- M/m to increase/decrease the integer you wish to factor
- Q/q to increase/decrease the number of qubits
- A/a to increase/decrease the value of $a$