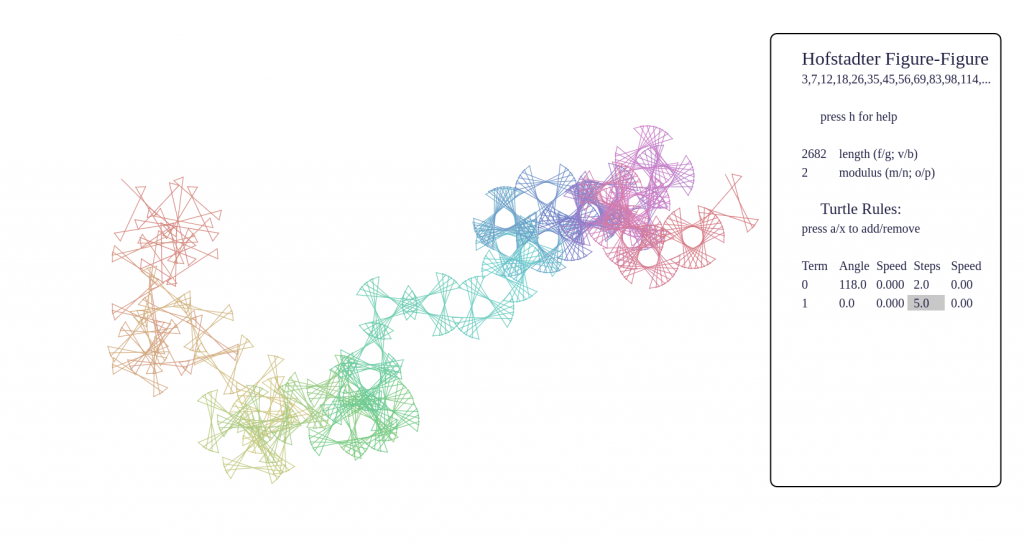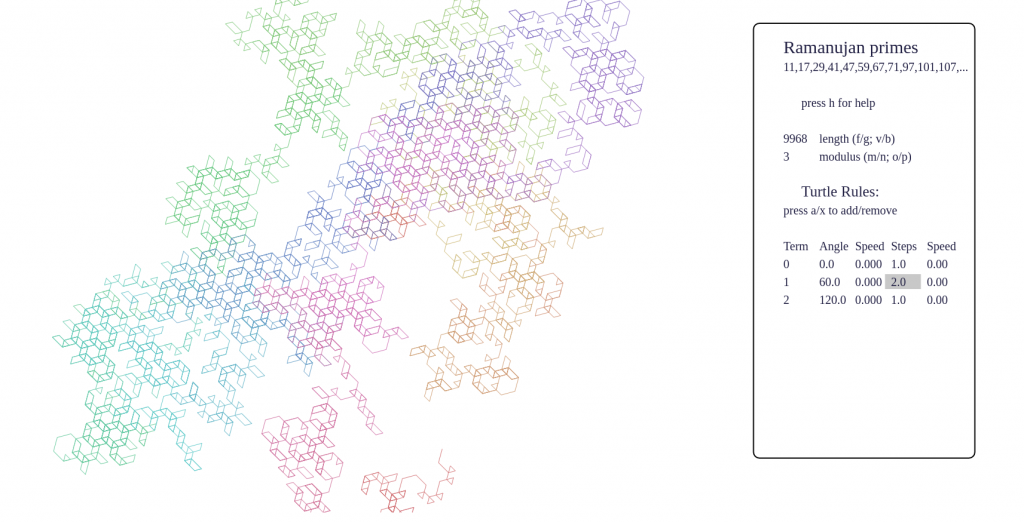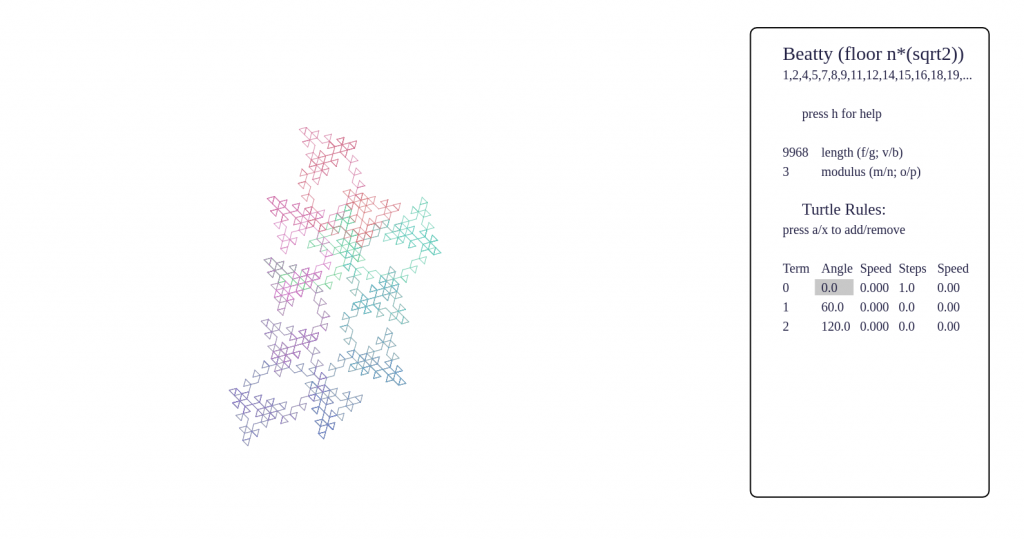This page contains a prototype of the Turtle on a Sequence, a tool for detecting self-similarity and divisibility relations between a sequence and its subsequences. This is part of Numberscope. This is a prototype, please expect bugs!
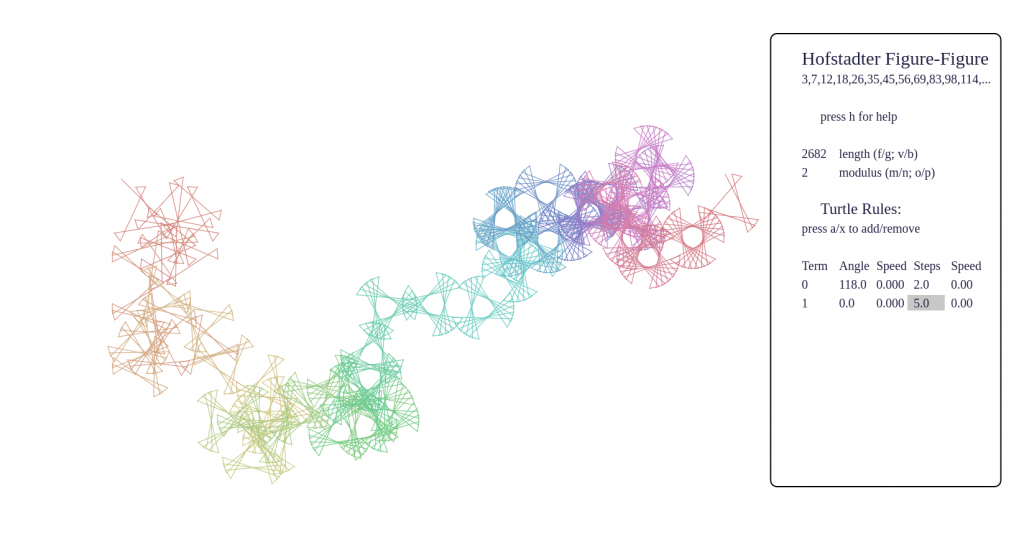
To launch the prototype, open the following link in Chrome (or another browser supporting the new implementation of bigint in Javascript): Turtle on a Sequence.
Give it a minute to load!
Some tips and tricks:
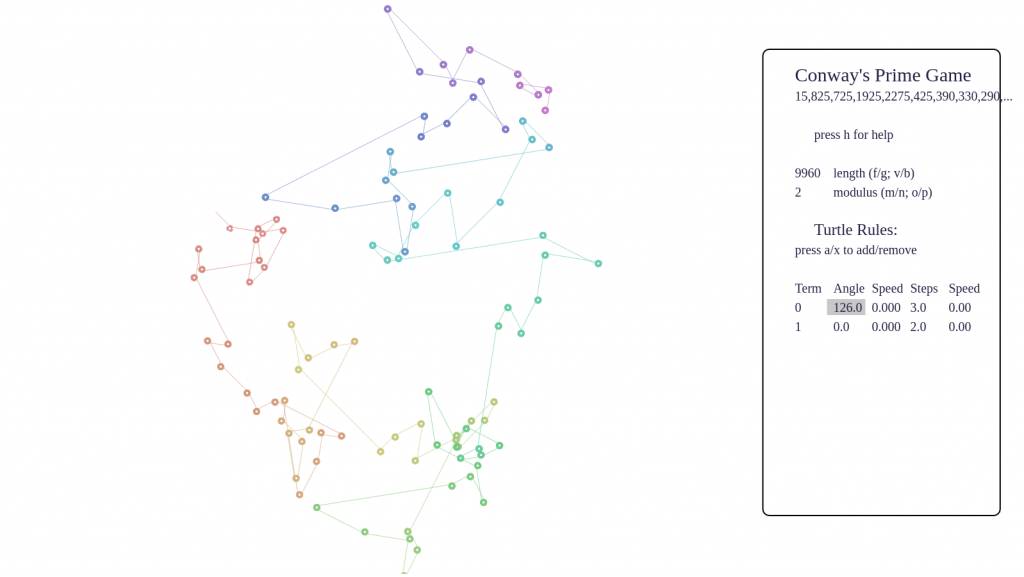
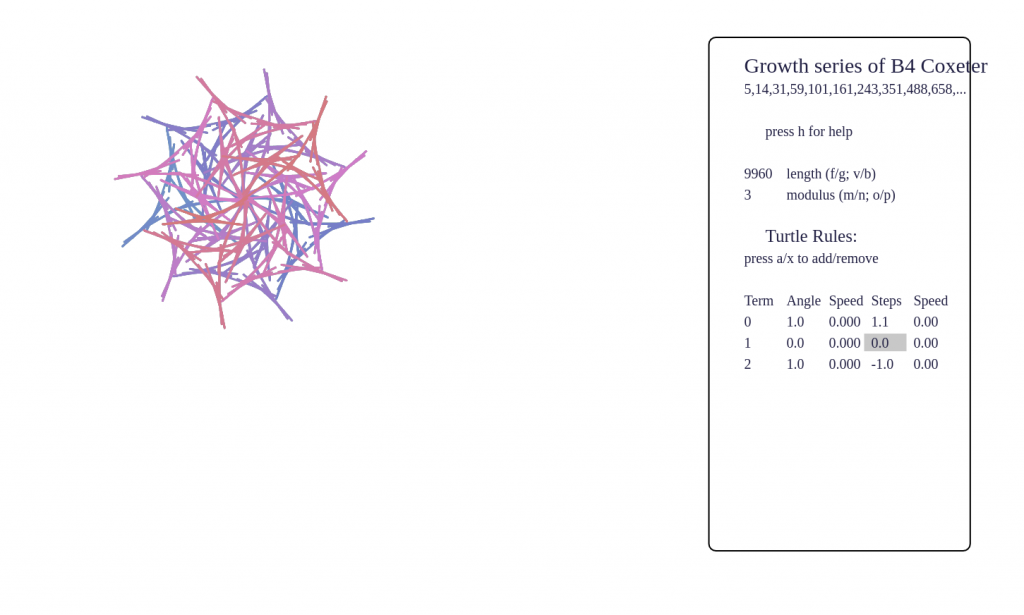
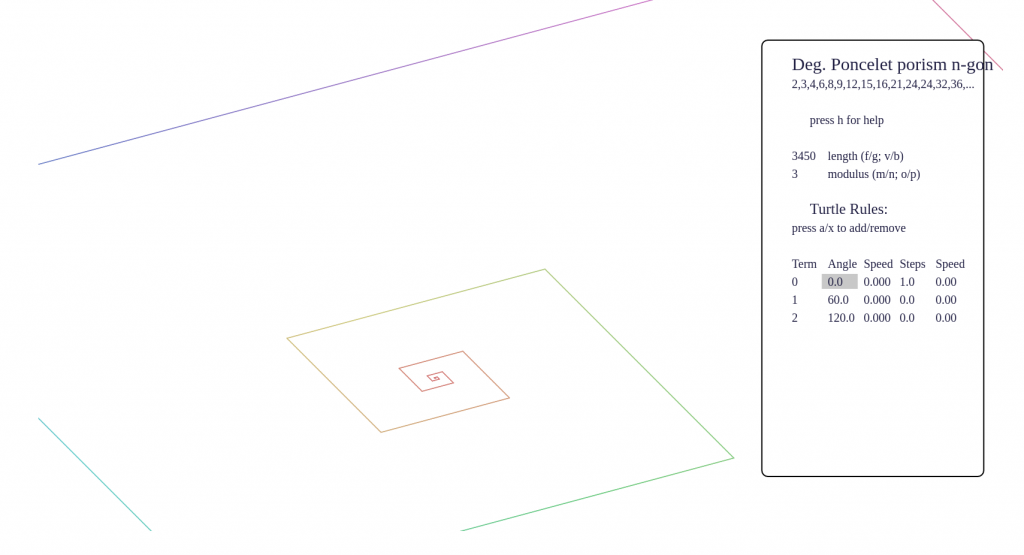
- To understand the screen in default setup, imagine a tiny turtle starts at the origin, and follows a set of rules which turn terms of the sequence into instructions to turn and step forward. The rules are listed at the right side of the page.
- To get started seeing some pretty pictures, I suggest tapping 9 and 0 to cycle forward and backward through some interesting presets. You can also tap e and r to cycle forward and backward through the full set of several dozen hard-coded sequences.
- Things you can do:
- Set a modulus to consider the sequence modulo. (Otherwise large terms are discarded.)
- Add and remove rules (press a and x).
- Change rules: use arrow keys to highlight a part of a rule and use +/- to change its value.
- zoom, pan, thicken lines, change colour
- increase/decrease number of terms
- set the rules to change at a certain rate, so the picture morphs
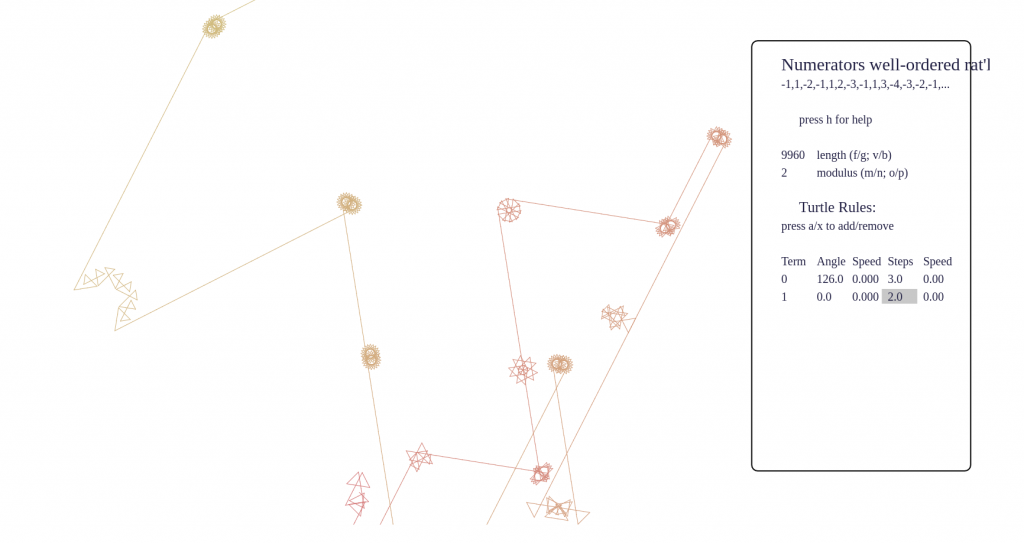
- What are you seeing? Beware that it is very easy to see structure in nothingness! Even a random sequence will appear patternful with certain turtle rules. For example, setting angles only to 120 and 60, and using only integer step values, a random walk will gradually fill out a triangular lattice. Some phenomena I’ve noticed are:
- if one rule has a large angle and another does not, you will tend to pick up visually the length of subsequences that call those rules consecutively; this can lead to little circles separated by long lines, for example
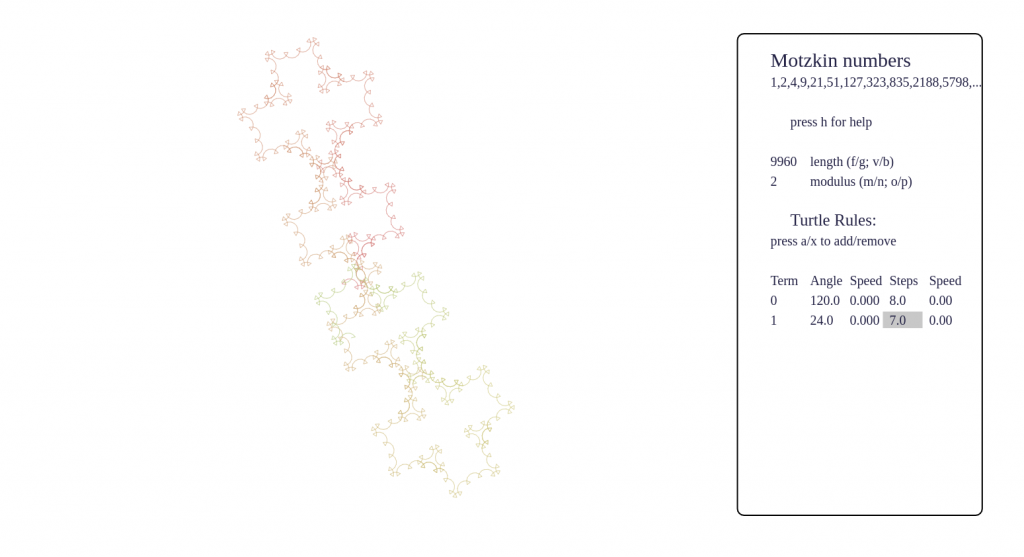
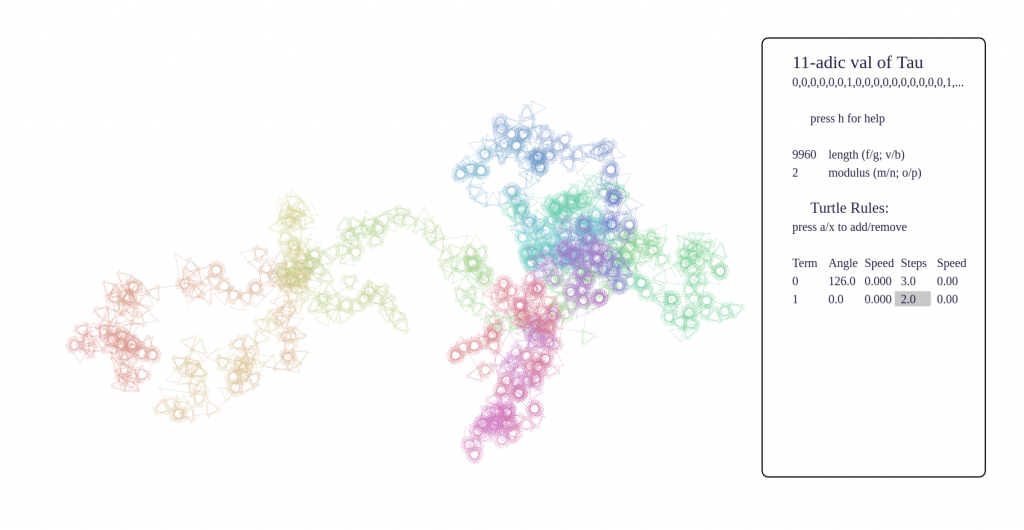
- certain sequences have fractal behaviour, such as p-adic valuations, Thue-Morse, Beatty sequences, and these produce very pleasing pictures
- periodicity will also be very apparent, either by a finite picture, or a picture that walks off one direction with the same pattern repeated
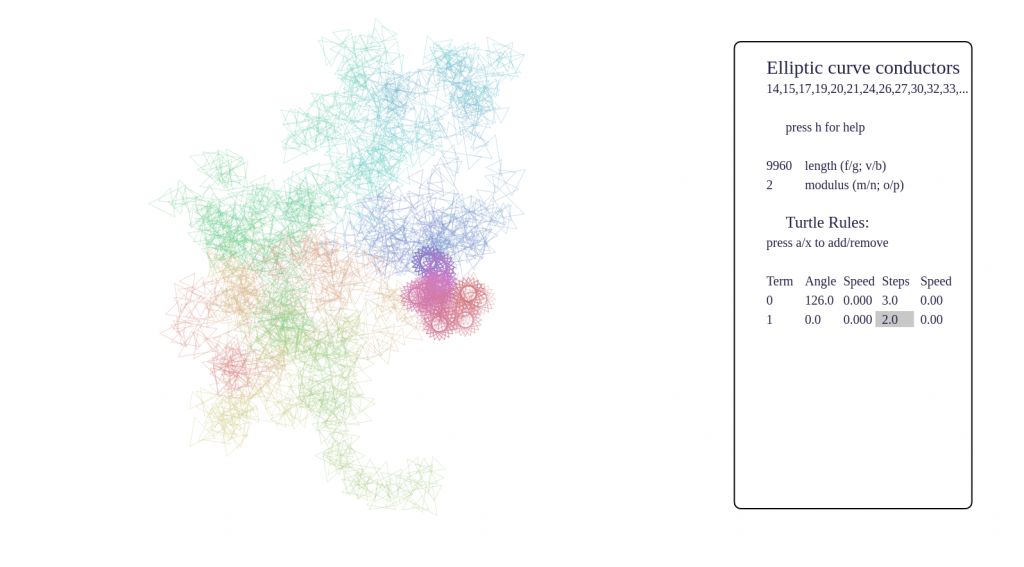
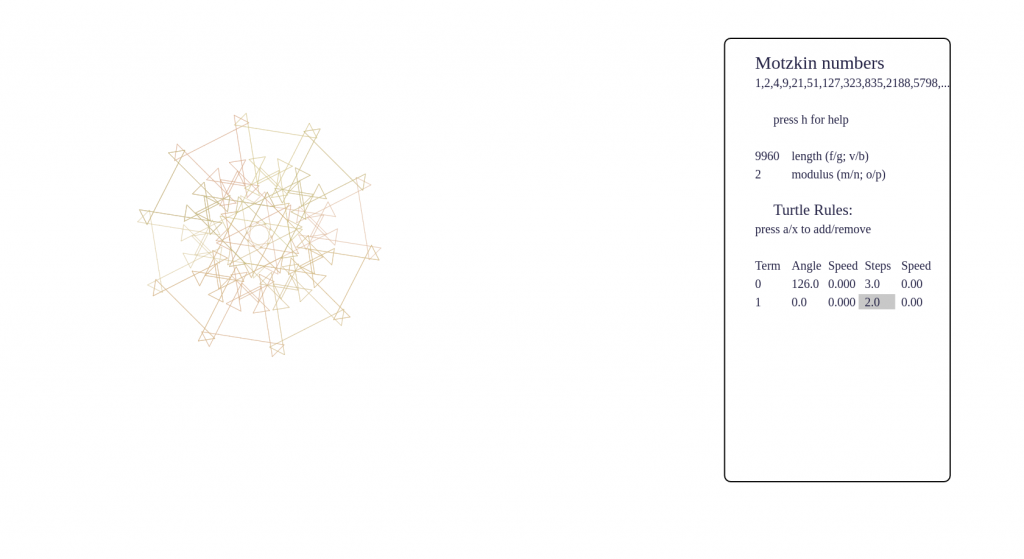
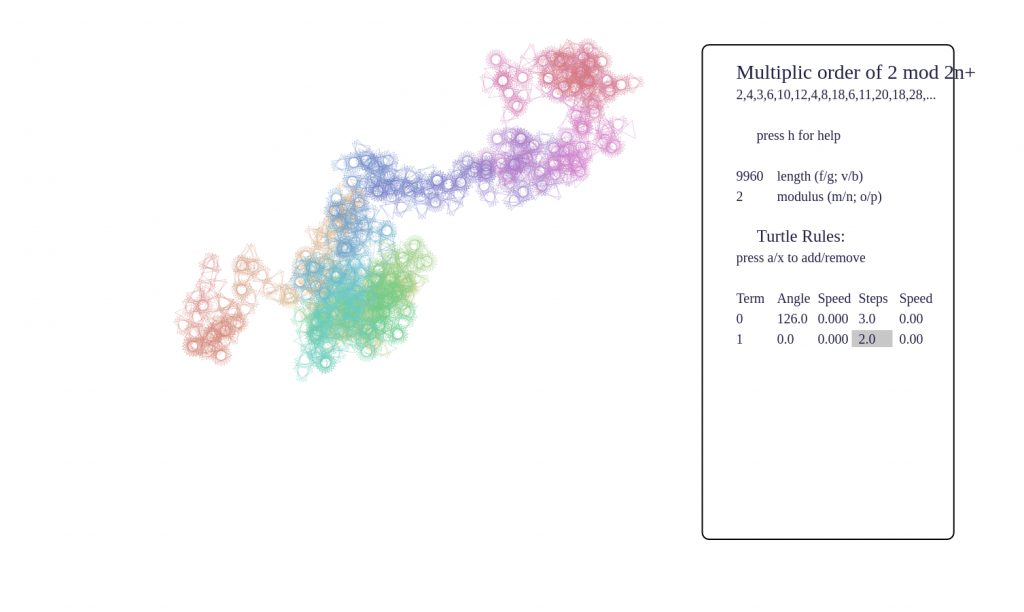
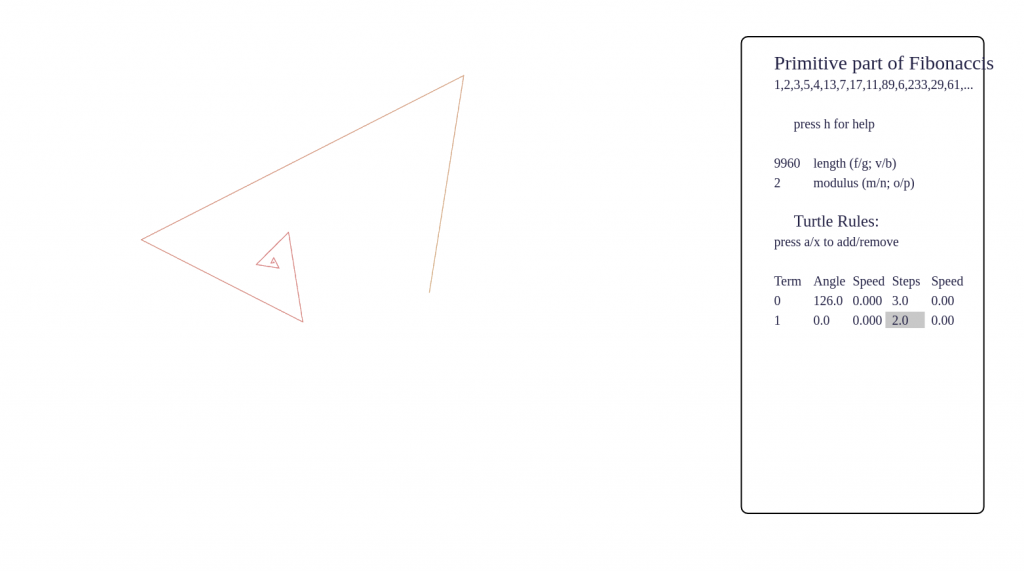
Some screenshots